Wuando presiona “enviar” en un mensaje de texto, es fácil imaginar que la nota viajará directamente desde su teléfono al de su amigo. De hecho, generalmente realiza un largo viaje a través de una red celular o Internet, los cuales dependen de una infraestructura centralizada que puede resultar dañada por desastres naturales o cerrada por gobiernos represivos. Por temor a la vigilancia estatal o la interferencia, los manifestantes expertos en tecnología en Hong Kong evitaron Internet mediante el uso de software como FireChat y Bridgefy para enviar mensajes directamente entre teléfonos cercanos.
Estas aplicaciones permiten que una misiva salte silenciosamente de un teléfono a otro, y eventualmente conecta al remitente con el receptor, los únicos usuarios capaces de ver el mensaje. Las colecciones de teléfonos enlazados, conocidas como redes en malla o redes móviles ad hoc, permiten un modo de comunicación flexible y descentralizado. Pero para que dos teléfonos se comuniquen, deben estar vinculados a través de una cadena de otros teléfonos. ¿Cuántas personas esparcidas por Hong Kong necesitan estar conectadas a través de la misma red de malla antes de que podamos estar seguros de que la comunicación entre ciudades es posible?

Una rama de las matemáticas llamada teoría de la percolación ofrece una respuesta sorprendente: solo unas pocas personas pueden marcar la diferencia. A medida que los usuarios se unen a una nueva red, poco a poco surgen focos aislados de teléfonos conectados. Pero la comunicación completa de este a oeste o de norte a sur aparece de repente cuando la densidad de usuarios supera un umbral crítico y agudo. Los científicos describen un cambio tan rápido en la conectividad de una red como una transición de fase, el mismo concepto que se usa para explicar cambios abruptos en el estado de un material, como el derretimiento del hielo o la ebullición del agua.
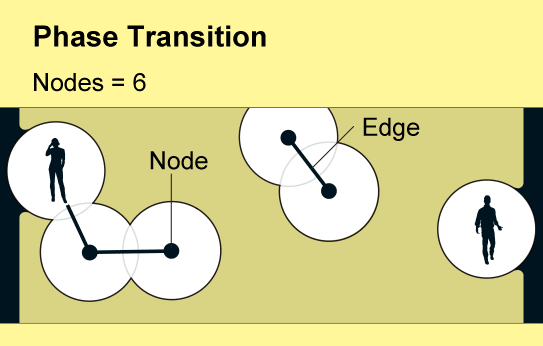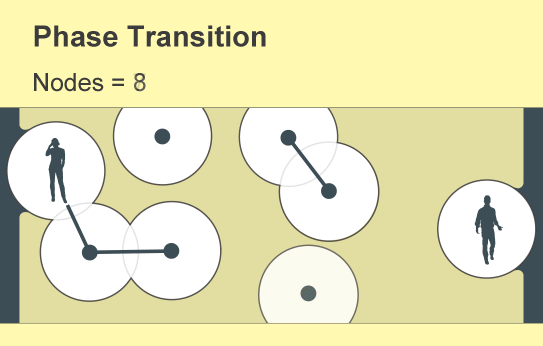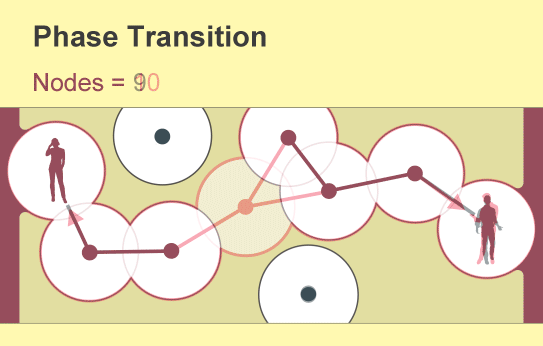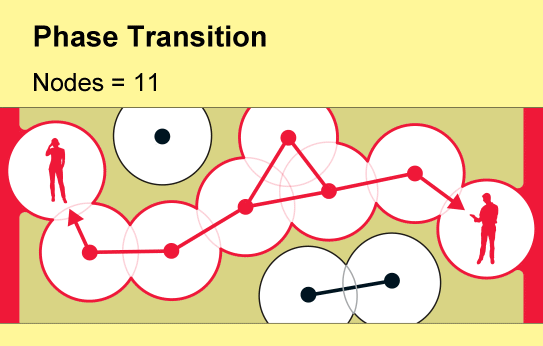
La teoría de la filtración examina las consecuencias de la creación o eliminación aleatoria de vínculos en tales redes, que los matemáticos conciben como una colección de nodos (representados por puntos) unidos por “bordes” (líneas). Cada nodo representa un objeto como un teléfono o una persona, y los bordes representan una relación específica entre dos de ellos. La idea fundamental de la teoría de la percolación, que se remonta a la década de 1950, es que a medida que aumenta gradualmente el número de enlaces en una red, surgirá de repente un grupo global de nodos conectados.
La pregunta que los científicos luchan por responder es: ¿Cuándo? ¿Cuál es el equivalente, para una red dada, de los cero grados Celsius a los que se derrite el hielo o los 100 grados C a los que hierve el agua? ¿En qué momento un meme se vuelve viral, un producto domina un mercado, comienza un terremoto, una red de teléfonos celulares logra una conectividad total o una enfermedad se convierte en una pandemia? La teoría de la filtración proporciona información sobre todas estas transiciones.
Los matemáticos suelen estudiar redes idealizadas, simétricas en geometría e infinitas en extensión, porque son las que se prestan a los cálculos teóricos. Las redes infinitas son generalmente las únicas con transiciones de fase realmente nítidas. Las redes del mundo real tienen un alcance limitado, a menudo son desordenadas y requieren cálculos desafiantes, pero también tienen transiciones, aunque más redondeadas. A medida que el mundo se conecta cada vez más a través de capas complejas de enlaces que transportan a las personas, les proporcionan energía a través de redes eléctricas o las conectan a través de las redes sociales, y en ocasiones propagan enfermedades entre ellas, la teoría de la filtración se vuelve cada vez más pertinente.
ENCAJAR EN SU LUGAR
En 1957, los matemáticos británicos Simon Ralph Broadbent y John Michael Hammersley enmarcaron por primera vez la teoría de la percolación como un problema puramente matemático. Resumieron el estudio de la percolación en química, que describe un fluido que se filtra a través de un material, como el aceite que se filtra a través de una roca porosa o el agua que se filtra a través del café molido. La red de percolación de una capa de roca consta de pequeños agujeros en su estructura, representados como nodos, junto con los canales o grietas que permiten que el fluido fluya entre ellos, representados como bordes. Como era de esperar, el petróleo fluye más a través de la roca que está más fracturada. Utilizando la teoría de la percolación, Broadbent y Hammersley predijeron que en una roca idealizada, el petróleo pasará de fluir solo a través de pequeñas regiones a impregnar repentinamente casi toda la roca cuando la densidad de las grietas supere un cierto umbral.
Los geólogos utilizan una versión de la teoría de la percolación para estudiar los tamaños de los racimos en la roca fracturada, que es relevante para la extracción de petróleo mediante fracturación hidráulica y la ocurrencia de terremotos. Para modelar terremotos, los sismólogos crean redes de percolación que coinciden con la escala y densidad de las grietas observadas, y luego toman en cuenta las tensiones ajustando la probabilidad de que las grietas se conecten. A medida que aumentan las tensiones y los vínculos, los grupos se expanden hasta que, repentina e impredeciblemente, estalla un terremoto. Las versiones modificadas del proceso de percolación permiten que las grietas se curen y refracturen para simular réplicas o cambios a largo plazo.
La teoría de la percolación también ilumina los procesos físicos y químicos en una escala mucho más pequeña, como la polimerización , el proceso mediante el cual moléculas pequeñas y simples llamadas monómeros se unen para formar grupos más grandes llamados polímeros. En el marco de la teoría de la percolación, cada monómero actúa como un nodo y dos vecinos pueden formar espontáneamente un enlace o borde. Si aumenta la probabilidad de que se unan, el sistema eventualmente alcanzará el umbral de percolación y emergerá un polímero gigante conectado. Este proceso es lo que hace que la gelatina en polvo disuelta en agua se asiente y forme gelatina.
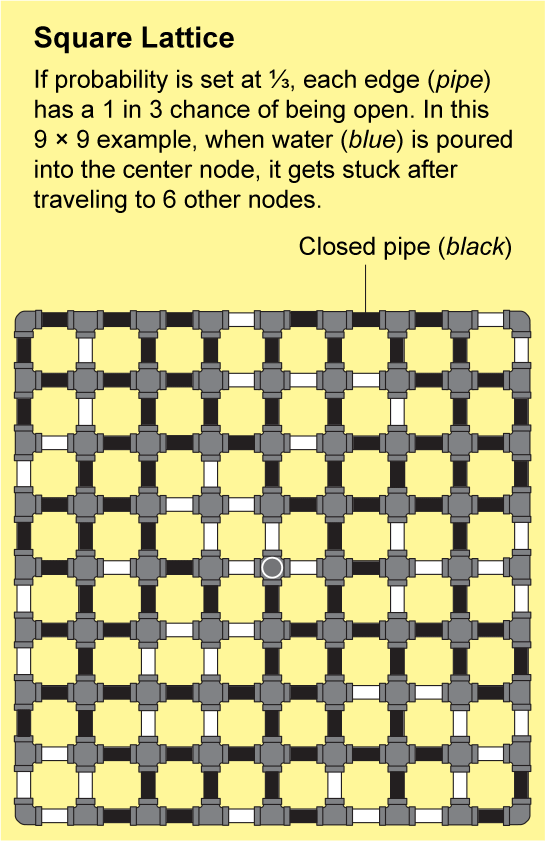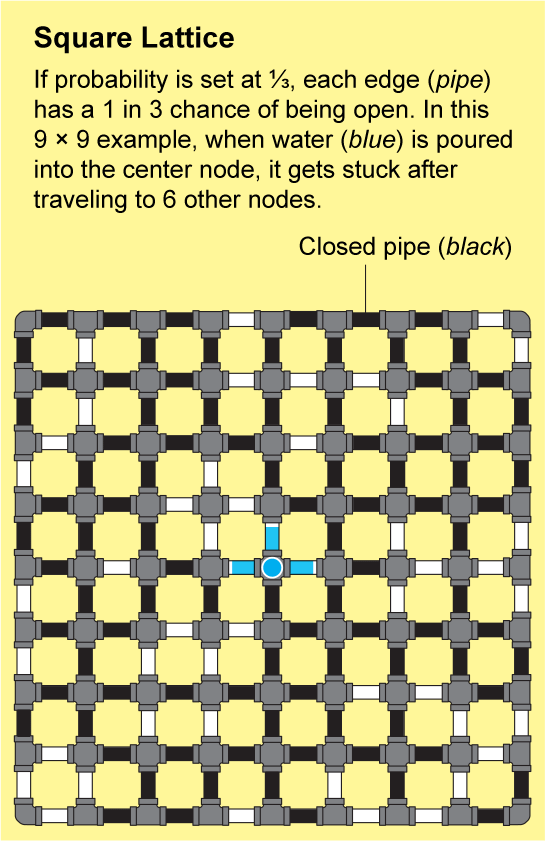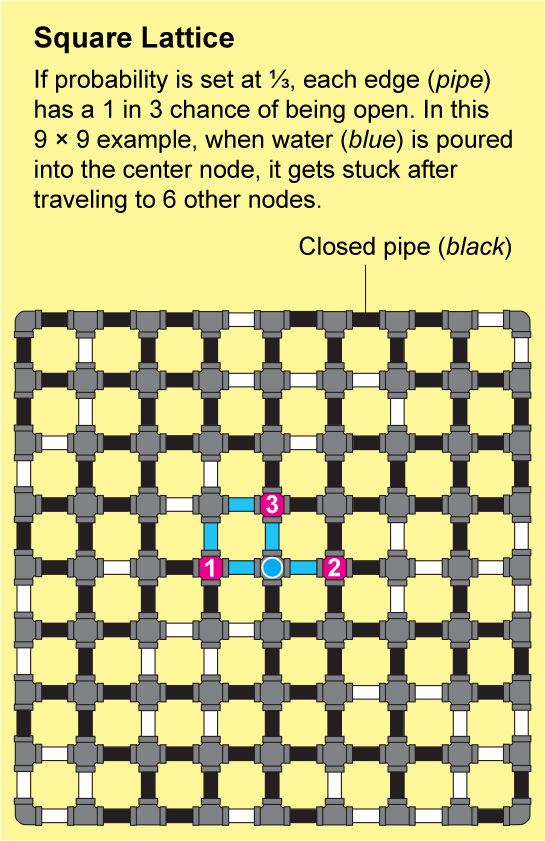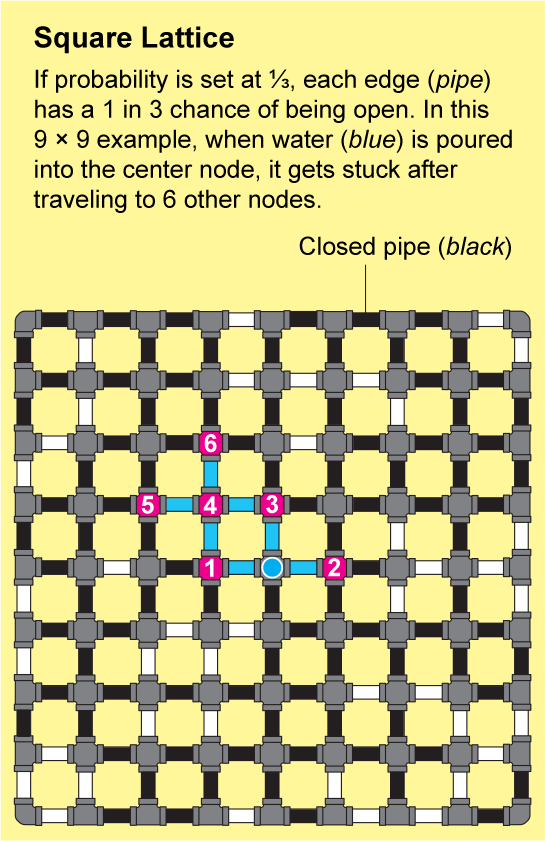
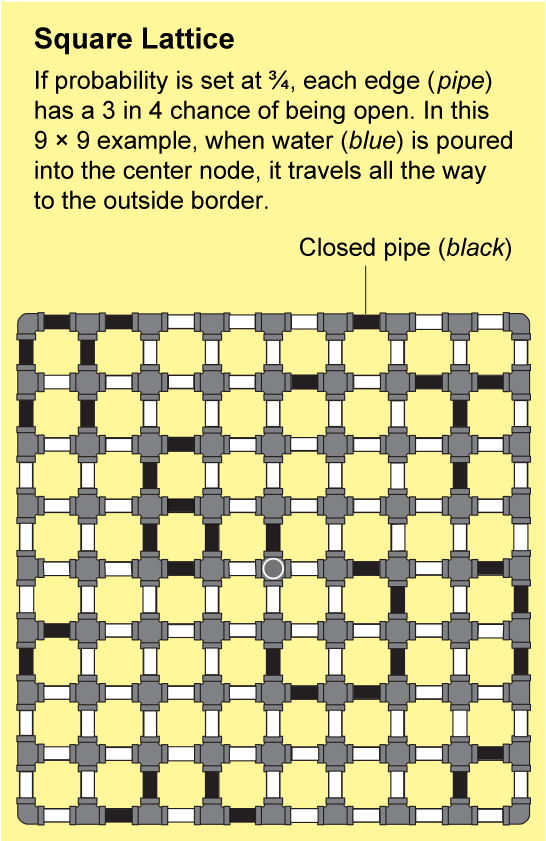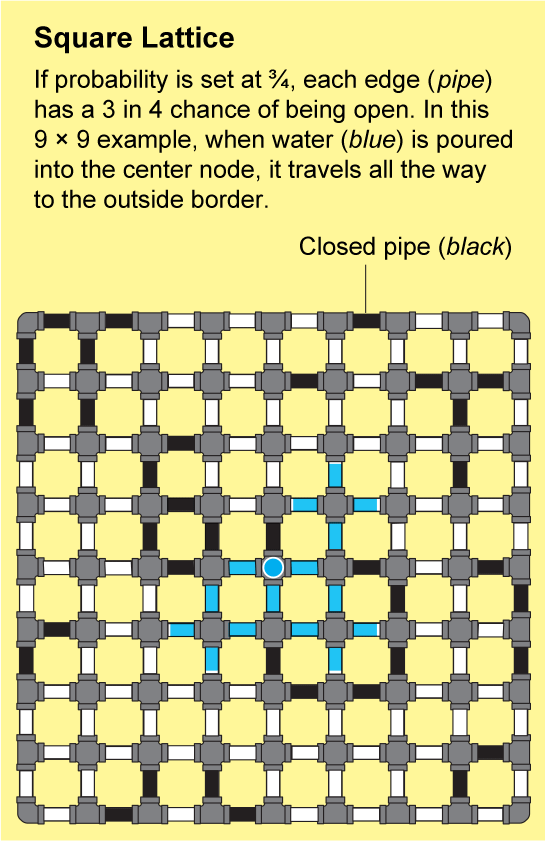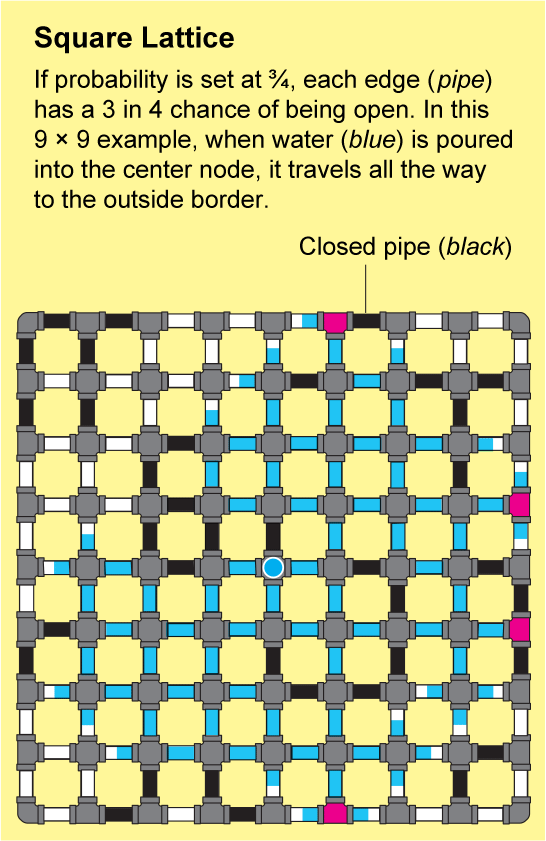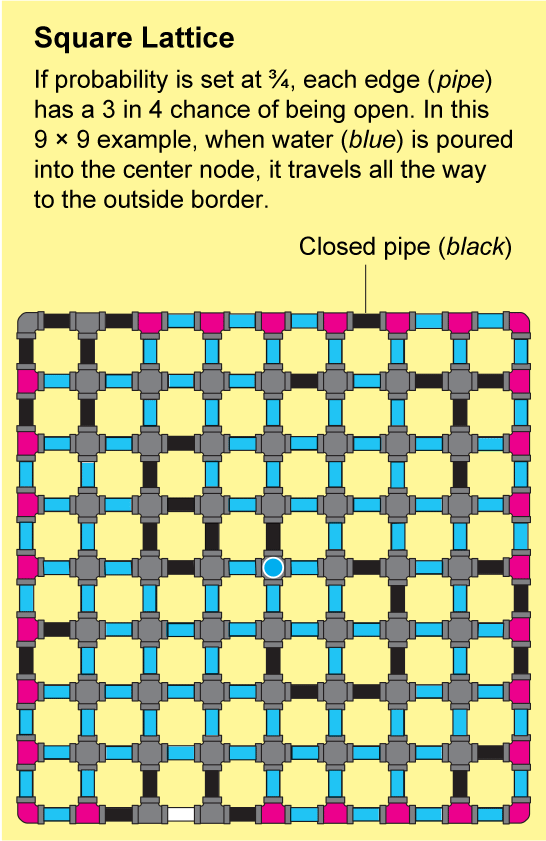
Las redes en la roca fracturada o los polímeros enlazados son extremadamente intrincadas. Sería casi imposible describir su estructura con precisión, pero Broadbent y Hammersley demostraron que pueden aproximarse mediante patrones repetidos que son susceptibles de análisis. El ejemplo más simple es una celosía cuadrada, que parece una hoja interminable de papel cuadriculado: los nodos están dispuestos en una cuadrícula y están conectados por cuatro bordes a sus vecinos.
Para ver cómo puede viajar un fluido a través de esta red, imagine que cada borde diminuto del papel cuadriculado es una tubería abierta o cerrada. Podemos determinar el estado de cada tubería lanzando una moneda etiquetada como “abierta” en un lado y “cerrada” en el otro. El paisaje resultante de tuberías abiertas y cerradas será una red aleatoria, y tendrá algunos grupos “abiertos” en los que todos los nodos están conectados por una serie de tuberías abiertas. Si vertiera agua en cualquier nodo de dicho grupo, fluiría a través de las tuberías abiertas para llegar a todos los demás nodos de ese grupo.
La teoría de la filtración se ocupa de la conectividad de la red, que corresponde al tamaño de los clústeres abiertos. Pero “grande” es un concepto ambiguo que no se presta fácilmente a las formalidades de las matemáticas. Entonces, los matemáticos a menudo sustituyen grandes números con infinito. La pregunta central entonces es: ¿Existe un cúmulo infinito? “Para nosotros, es mucho más fácil responder a esta pregunta de sí o no que responder cuántos grupos grandes vemos de este o este tamaño”, dice Benedikt Jahnel, matemático del Instituto Weierstrass de Análisis Aplicado y Estocástica en Berlín. .
De hecho, la probabilidad de que una red infinita tenga un clúster infinito es siempre del 0 o del 100 por ciento. Esto se debe a que el proceso de filtración está sujeto a un principio general en la teoría de la probabilidad llamado ley cero-uno, descubierto por el matemático ruso Andrey Kolmogorov en la década de 1930. Suponga que lanza una moneda un número infinito de veces. La ley cero-uno se refiere a cualquier pregunta sobre el resultado cuya respuesta no dependa de un número finito de cambios. (Por ejemplo, la respuesta a la pregunta: “¿Aterrizaste con cara infinitas veces?” No cambiará si modificas un número finito de lanzamientos de moneda, pero la respuesta a la pregunta “¿Aterrizaste con cara en la tercera lanzar? ”se puede cambiar modificando solo un lanzamiento de moneda).
La ley cero-uno nos dice que los cambios finitos no pueden perturbar fenómenos que son de naturaleza infinita. Por tanto, la probabilidad de encontrar un grupo infinito en una red infinita no puede cambiar ligeramente, como de 0,81 a 0,82; debe tomar una de las posiciones extremas, cero o uno. Para decirlo de otra manera, una red infinita no tendrá un grupo infinito (una probabilidad de cero para encontrar un grupo infinito) o tendrá un grupo infinito (una probabilidad de uno).
Por lo tanto, cambiar un número finito de tuberías abiertas a tuberías cerradas, o viceversa, no tiene ningún efecto sobre si existe un grupo abierto infinito. La probabilidad de encontrar un grupo infinito es cero o uno. Cual es
ENCONTRAR EL UMBRAL
La respuesta depende del sesgo de su moneda. Imagina que tienes un dial que controla el sesgo. Cuando el dial se gira completamente hacia la izquierda, la moneda siempre aterrizará en “cerrado”. Una vez que todas las tuberías estén cerradas, el agua vertida en un nodo no fluirá a ninguna parte y la probabilidad de encontrar un grupo infinito será cero. A medida que gira el dial en el sentido de las agujas del reloj, aumenta la probabilidad de que la moneda caiga en “abierto”, y con lanzamientos adicionales habrá más y más tubos abiertos. Cuando el dial se gira completamente hacia la derecha, la moneda siempre aterrizará en “abierto” y, finalmente, el agua vertida en un nodo fluirá hacia el resto. La probabilidad de encontrar un grupo infinito es entonces uno.
Si gira lentamente el dial en el sentido de las agujas del reloj, la probabilidad de que las tuberías se abran aumenta gradualmente, y podría parecer que la posibilidad de encontrar un grupo infinito también debería aumentar gradualmente de cero a uno. De hecho, el cambio ocurre instantáneamente debido a la ley cero-uno: establece que la probabilidad no puede estar entre cero y uno. Para el retículo cuadrado, la probabilidad pasa de cero a uno cuando el cuadrante está exactamente en el medio, cuando la moneda no tiene sesgo. Esta posición crítica del dial se conoce como umbral de percolación. No importa cuál sea la forma de la red, ya sea, por ejemplo, una celosía triangular o una versión tridimensional de la celosía cuadrada, la cuestión esencial de la teoría de la percolación sigue siendo la misma: ¿Dónde está el umbral? ¿Qué nivel de sesgo debe tener la moneda antes de que se abran suficientes enlaces para garantizar un cúmulo abierto infinito?
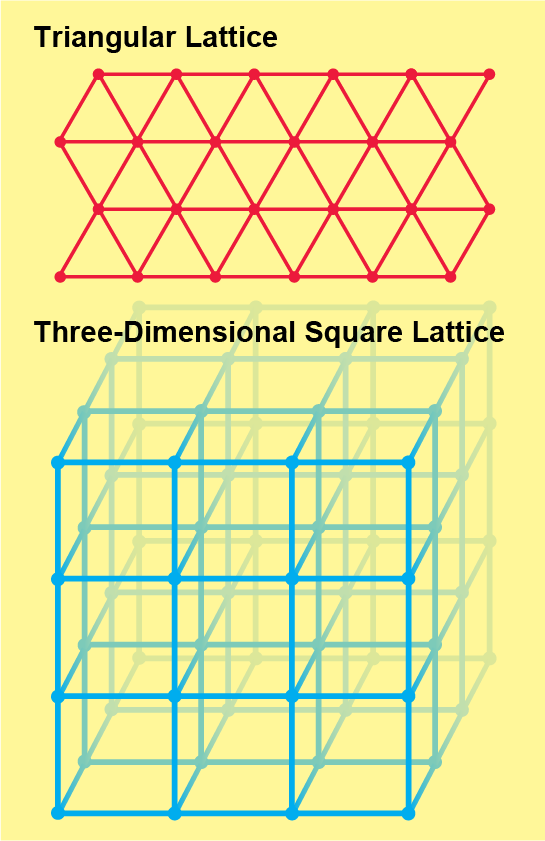
La respuesta depende de la forma exacta de la red (infinita) y está lejos de ser fácil de encontrar. Incluso probar que el umbral para una celosía cuadrada, el sistema más simple, es la mitad, fue un desafío abrumador, finalmente resuelto por el matemático Harry Kesten en 1980. Y a pesar de décadas de esfuerzo, los umbrales de percolación exactos se conocen solo para unas pocas redes extremadamente simples . “Se ha realizado un montón de trabajo para encontrar cuál es el umbral”, dice Robert M. Ziff, físico estadístico de la Universidad de Michigan. “Es alucinante cuántos sistemas diferentes ha visto la gente”. Ziff armó una página de Wikipedia documentar los umbrales de percolación para cientos de redes diferentes. El sesgo de la celosía triangular es aproximadamente 0.347, un número determinado analíticamente, pero la gran mayoría de los números en esa página (incluido el sesgo de umbral de una celosía cuadrada tridimensional) son aproximaciones derivadas de simulaciones por computadora.
REDES DE MALLA
Las celosías son buenos modelos para la percolación en sistemas físicos como la roca fracturada, donde los agujeros están en ubicaciones fijas y las grietas entre ellos se forman al azar. Pero otras redes del mundo real son mucho más complicadas. En las redes de malla FireChat y Bridgefy mencionadas anteriormente, por ejemplo, las ubicaciones de los nodos, los teléfonos que llevaban los manifestantes de Hong Kong, cambiaban constantemente. Los bordes en una red de este tipo, o conexiones, se forman cuando dos teléfonos están lo suficientemente cerca el uno del otro, dentro del rango de decenas de metros de las aplicaciones basadas en Bluetooth que se usan para compartir mensajes. Estas redes se describen mediante un modelo diferente, llamado percolación continua, porque los nodos de la red en malla pueden estar en cualquier lugar de un espacio continuo.
Como cualquier modelo matemático, la versión abstracta de esta red se basa en supuestos simplificados. Los teléfonos inteligentes están dispersos al azar, sin imitar los grupos y patrones naturales en un mapa de los meandros de las personas, y dos teléfonos inteligentes están vinculados solo en función de su distancia entre sí, sin tener en cuenta las paredes u otras interferencias. No obstante, el modelo destaca el papel central que juega la teoría de la percolación en las redes de malla reales.
Hay dos formas de aumentar la conectividad de esta red de percolación continua: habilitar la conexión directa en un rango más largo o agregar más teléfonos inteligentes, aumentando la densidad de usuarios. Estas modificaciones pueden considerarse diales como los descritos para la red de tuberías; girar cualquiera de los dos en el sentido de las agujas del reloj aumentará la conectividad. Y en estos modelos, “hay un cambio en el que realmente se pasa de la conectividad local a la global”, dice Jahnel.
Para los diseñadores de aplicaciones de redes de malla, encontrar el umbral de percolación es un problema práctico de ingeniería. Cambiar la potencia del dispositivo, que controla el rango, es una forma de girar un dial. La pregunta central, dice Ram Ramanathan, científico jefe de la empresa de redes de malla goTenna, es: “¿Cuál quiere que sea la potencia de transmisión para tener una red conectada?” La respuesta sería bastante simple si la potencia y la conectividad tuvieran una relación lineal, si cada pequeño aumento de potencia condujera a un pequeño aumento proporcional de la conectividad. Pero la existencia de un umbral de filtración significa que existe el riesgo de que la red pierda repentinamente la conectividad a medida que las personas se mueven. La potencia óptima es aquella que garantiza que la red esté siempre conectada pero que no desperdicie energía.
El otro dial es la densidad de teléfonos. Las redes de malla con un rango fijo necesitan una densidad crítica de usuarios y es más probable que proporcionen una conectividad generalizada en eventos concurridos como un festival de música, un partido de fútbol o una gran protesta. Jorge Ríos, CEO y cofundador de Bridgefy, dice que la compañía vio grandes picos de nuevos usuarios en Cachemira, Nigeria, Hong Kong e Irán durante períodos de disturbios civiles, cuando la gente recurrió a redes de malla para mantener las comunicaciones en caso de que el gobierno cerrara. Internet o grandes multitudes bloquearon las conexiones celulares. Algunos vecindarios, como Red Hook en Brooklyn, NY, están utilizando redes de malla para expandir el acceso a Internet mediante la fijación de nodos permanentes en la parte superior de los edificios. Gran parte del hardware y la tecnología de enrutamiento necesarios aún están evolucionando, pero es fácil imaginarse audaces,
REDES DE CONTACTO DE ENFERMEDADES
Las redes utilizadas para modelar el flujo de petróleo a través de rocas o la comunicación directa entre teléfonos imitan la estructura espacial real de estos sistemas: dos nodos están conectados por un borde si los objetos que representan están cerca uno del otro en el espacio físico. Pero para las redes que rastrean la propagación de enfermedades de persona a persona, los vínculos están determinados por las formas en que ese germen específico se transmite entre ellas. Dichas redes están particularmente enredadas: una persona infectada que pasa una hora en un club nocturno en una gran ciudad puede transmitir un virus a una persona que lo transmite por todo el país o incluso a través de los continentes en los días siguientes.
Los modelos epidemiológicos más simples agrupan a todos en tres grupos: susceptibles, infectados y recuperados, y descuidan esta compleja estructura de conexiones. En tales modelos, las personas infectadas transmiten la enfermedad a otras al azar en el grupo susceptible bajo el supuesto de que todos en ese grupo (estudiantes en un dormitorio o residentes en una ciudad) tienen la misma probabilidad de contraerla. La tasa a la que las personas susceptibles se infectan depende del número reproductivo básico, el número promedio de nuevas infecciones causadas por una sola persona infectada, abreviado como R 0 . Si R 0 es mayor que uno, entonces el virus se está propagando, y si es menor que uno, el brote se está extinguiendo.
En la práctica, sin embargo, la forma en que las personas interactúan influye en la propagación general de la enfermedad. Por ejemplo, un brote de síndrome respiratorio agudo severo, o SARS, en 2003, tuvo inicialmente valores de R 0 entre 2.2 y 3.6, pero los recuentos de casos fueron “mucho más bajos de lo esperado durante este período, como sugiere un simple cálculo”, escribió Lauren Ancel Meyers. , ahora director del Consorcio de Modelado COVID-19 de la Universidad de Texas, en un artículo de 2006 . La discrepancia, argumentó, se deriva de la suposición de que “todos los individuos susceptibles tienen la misma probabilidad de infectarse”, lo que ignora la forma compleja de las redes de contacto de las personas. En particular, el R 0 estimadoLos valores del SARS se basaron en su rápida propagación dentro de los edificios de apartamentos y hospitales, que tienen “tasas anormalmente altas de contactos cercanos entre individuos” en comparación con la población general. Pero debido a que las personas infectadas con SARS se enfermaron muy rápidamente, terminaron en hospitales antes de que pudieran infectar a muchas personas fuera de ellos.
Los bordes de una red de enfermedades expresan relaciones específicas. En uno que muestra la posible propagación del VIH, por ejemplo, dos personas están conectadas por un borde si han intercambiado fluidos corporales. Una red que muestra la propagación potencial de COVID-19 tiene una estructura de bordes muy diferente, lo que representa un contacto cercano sin protección respiratoria. Los bloqueos o restricciones como el cierre de negocios y la limitación de viajes alteran esta estructura de borde y, junto con las máscaras y el distanciamiento físico, evitan que el virus salte de una persona o nodo a otro. Un desafío para los epidemiólogos es encontrar formas de desconectar suficientemente la red.
Las redes de contacto de enfermedades del mundo real, como las que muestran la propagación de COVID-19, son extremadamente complicadas y difíciles de describir con precisión. Incluso si se conociera la estructura exacta de la red, sería difícil analizarla matemáticamente. Se utilizan simulaciones por computadora y análisis de datos masivos para predecir números de casos futuros, evaluar el impacto de un metro frente a dos metros de distanciamiento social y cuantificar la importancia de las escuelas y los restaurantes en la propagación del coronavirus. Alessandro Vespignani, un teórico de redes complejas de la Northeastern University, se refiere a esta investigación como su trabajo “en tiempos de guerra”: táctico y ocasionalmente desordenado, pero que produce los resultados numéricos inmediatos que necesitan los encargados de formular políticas y los trabajadores de la salud. Vespignani y sus colegas crean “una especie de sociedad sintética en la que todos estos individuos se empaquetan en una computadora” para ejecutar simulaciones, dice.
Por el contrario, Vespignani se refiere a su investigación en “tiempos de paz” como el período en el que “desarrollas el modelo, calibras diferentes formas de modelar las cosas, desarrollas enfoques específicos, buscas cómo puedes mejorar tus resultados”. Para obtener una comprensión teórica de cómo la forma básica y las características estructurales de una red impactan en la propagación de una enfermedad, los científicos recurren a la teoría de la percolación.
Las herramientas que ofrecen las matemáticas tradicionales de la percolación con lápiz y papel funcionan solo en los casos más simples, donde la red está ordenada y simétrica artificialmente. Aun así, “las matemáticas son cruciales para guiar su comprensión”, dice Vespignani. Los epidemiólogos de la red reducen la red a lo esencial, en particular, la denominada distribución de grados. Un grado es el número de otros nodos a los que está conectado un nodo específico. En la celosía cuadrada, por ejemplo, todos los nodos tienen grado cuatro. Sin embargo, en una red de enfermedades, el grado varía drásticamente: algunas personas tienen muchos contactos y pueden transmitir la enfermedad a muchas personas, mientras que otras están bastante aisladas.
La distribución de grados describe la probabilidad de que un nodo tenga cada grado. En las redes de contacto de enfermedades, esto se traduce en la probabilidad de que alguien infecte (o sea potencialmente infectado por) un cierto número de otras personas. Para comprender cómo afecta este aspecto al umbral de percolación, los epidemiólogos matemáticos como Meyers generan miles de redes de muestras que son esencialmente aleatorias excepto por una característica: todas tienen la misma distribución de grados. Este enfoque es una forma de aislar la distribución de grados para percibir su papel en la estructura de la red. Si las propiedades de las redes generadas coinciden con las redes del mundo real, entonces la distribución de grados o cualquier otra característica que esté “incorporada en las matemáticas” probablemente sea relevante para la propagación de la enfermedad, dice Meyers. Si la pareja es perfecta,
La investigación muestra que el umbral de percolación de una red cae si la red tiene una distribución de grados más amplia, lo que significa un rango más amplio en los grados de los nodos. Por lo tanto, una enfermedad se propagará más fácilmente en una red con algunas personas altamente conectadas y algunas personas aisladas que en una red en la que todos tienen aproximadamente el mismo número de contactos. Joel Miller, epidemiólogo matemático de la Universidad La Trobe en Melbourne, Australia, explica la observación de manera heurística: “Si tengo 10 veces más contactos que tú, tengo 10 veces más probabilidades de infectarme y 10 veces más es probable que se propague como usted, por lo que es 100 veces más importante para la propagación de la enfermedad “.
REDES DEL FUTURO
La teoría de la filtración se utiliza para modelar otros fenómenos de “contagio”, como cuando un meme en una red social gana terreno lentamente antes de volverse viral de repente. Se puede aplicar a modelos económicos para mostrar cómo un producto en particular puede llegar rápidamente a dominar un mercado a medida que las personas comparten recomendaciones entre sus contactos sociales. Los modelos de votantes, en los que las personas influyen en su comunidad, también muestran efectos de umbral.
En contraste con las redes infinitas y perfectamente ordenadas que los matemáticos han estudiado tradicionalmente, las redes derivadas de ejemplos reales son finitas en extensión y desordenadas. Las redes finitas no saltan instantáneamente de estar conectadas dentro de pequeños bolsillos a estar conectadas casi en todas partes como lo hacen las redes infinitas, pero generalmente hacen el cambio muy rápido. Para comprender estos procesos, los teóricos de redes van y vienen entre las matemáticas y las simulaciones por computadora. Las redes más simples los guían en la construcción de modelos informáticos detallados de redes reales, lecciones de las cuales, a su vez, influyen en la forma en que modifican los modelos de lápiz y papel para obtener una visión del mundo real.
Muchos modelos de red importantes de la propagación de COVID-19 integran información de otras redes. Los sistemas escolares, las rutas de los trenes y los horarios de los empleados del hospital forman redes, y cada uno de ellos influye en el curso de la pandemia. “Vivimos en este sistema de redes interdependientes, y no podemos simplemente pensar en una sin comprender las consecuencias que traen las otras”, dice Raissa D’Souza, teórica de redes complejas en la Universidad de California, Davis. Cada red es su propio sistema complejo con su propio comportamiento emergente. Cada vez más, estamos acoplando estas redes para crear un sistema aún más complejo. Pero no existe un marco teórico claro para estudiar tales redes de redes. Comprender cómo sus propiedades se ven afectadas por las propiedades de las redes constituyentes es un desafío para el futuro.
“No vivimos en una burbuja o en un mundo completamente mixto. Vivimos en un mundo con contactos, seguimos cuentas de Twitter, y estos son lugares donde entran la percolación y otros modelos ”, dice Vespignani. Obtener una mejor comprensión de esos modelos matemáticos teóricos ahora “puede marcar la diferencia en el futuro”. Las redes de filtración son fácilmente adaptables, lo que genera nuevos campos de juego para los matemáticos y aplicaciones prácticas para los científicos, pero estos diversos modelos están unificados por una característica sorprendente: todos tienen un punto de giro agudo donde solo unas pocas conexiones nuevas unen la red. A medida que el mundo se vuelve cada vez más conectado, la necesidad de comprender estas transiciones cruciales se vuelve cada vez más urgente.
Fuente:
Houston-Edwards, K. (2021, 1 abril). The Mathematics of How Connections Become Global. Recuperado 16 de marzo de 2021, de https://www.scientificamerican.com/article/the-mathematics-of-how-connections-become-global/

